Entropy - Mathematics

What’s the most effective way to communicate a message? Before Claude Shannon's groundbreaking work in the 1940s, the focus was mainly on trying to distill meaning into its most compact form. However, this approach overlooked the true purpose of communication: to connect people. If two people already share the same information, there’s no reason to communicate at all.

Shannon’s key insight was that meaning itself doesn’t matter. Information is linked to unpredictability. The core of a message lies in its improbability.

Self-information and Entropy

To formalise this concept, Shannon introduced the idea of self-information. Mathematically, the self-information of an event with probability p is defined as:

\(I(p) = -\log p\)

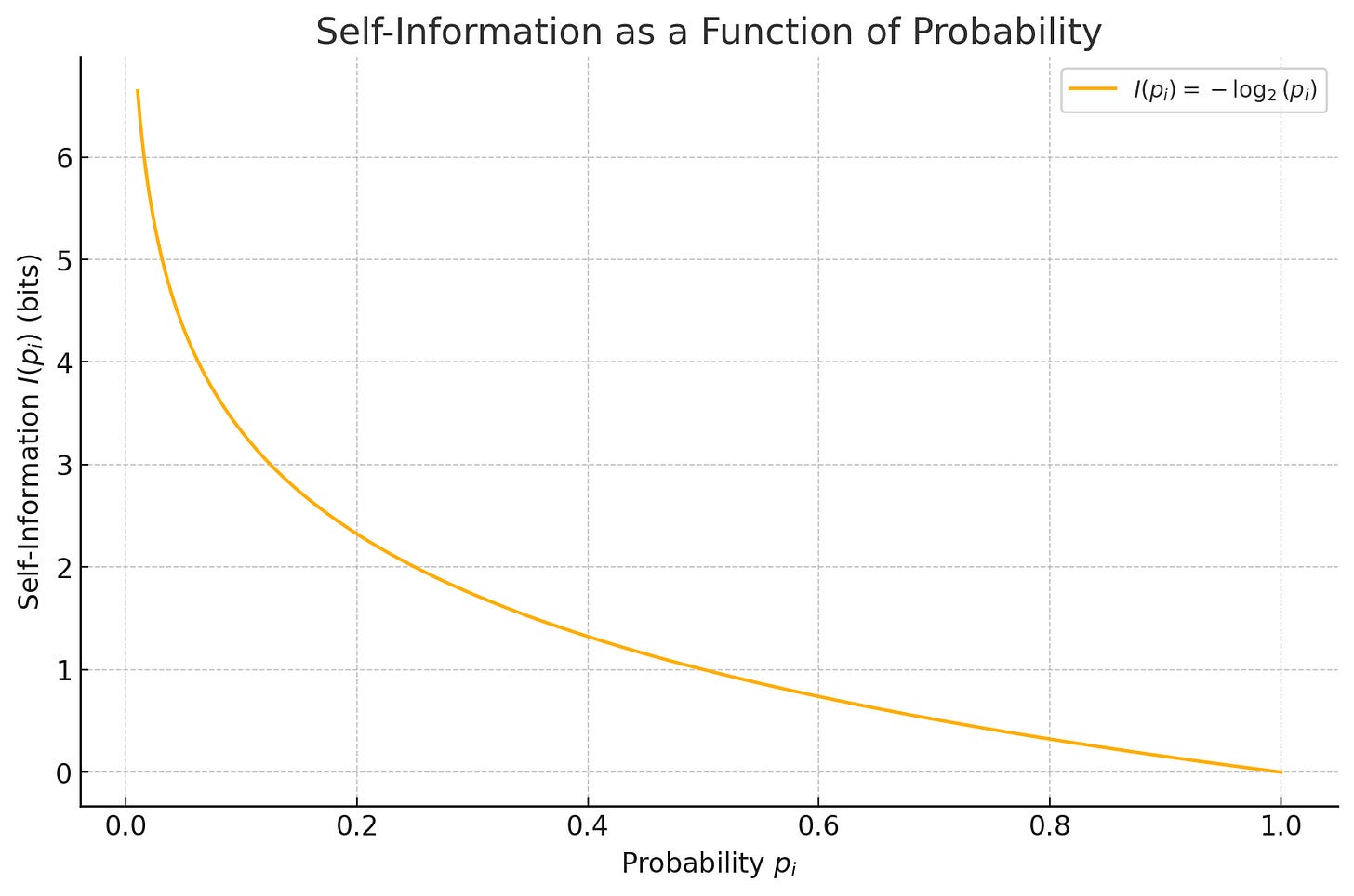
The plot shows the relationship between the probability p_i of an event and its self-information I(p_i). As the probability of an event decreases, its self-information increases. In other words, rare events provide more information than common ones.

Entropy H represents the average amount of information inherent in a set of possible outcomes. It is defined as the expected value of self-information:

\(H = \sum_{i} p_i \, I(p_i) = -\sum_{i} p_i \log p_i\)

KL Divergence and Cross Entropy

While entropy measures the information content of a single probability distribution, KL Divergence and cross entropy extends this concept to compare two distributions.

The Kullback-Leibler (KL) divergence measures how one probability distribution P diverges from a second probability distribution Q. It’s often used as a tool for model comparison.

\(D_{KL}(P \parallel Q) = \sum_{x \in X} p(x) \log\frac{p(x)}{q(x)}\)

Cross entropy is the sum of entropy and KL divergence.

\(H(P,Q) = H(P) + D_{KL}(P \parallel Q) = -\sum_{x \in X} p(x) \log q(x)\)

Cross entropy is asymmetric, meaning H(P, Q) is generally not equal to H(Q, P). When P and Q are identical, cross entropy reduces to entropy. This measure is widely used as a loss function in training machine learning models.

The lessons of Entropy

Understanding entropy provides valuable insights for communication:

1. Focus on the unexpected: Information is most valuable when it's surprising. Don't waste time conveying what your audience already knows.

2. Ignore the noise: Don't try to extract key information from "bullshit." Recognising low-entropy content can help us focus on what's truly informative.